Modelo probabilístico, comunes (teoría).
Puedes descargar el tema completo aquí:tema_4.pdf (960054)
Modelo probabilísticos
Modelo probabilístico, es la forma que pueden tomar un conjunto de datos obtenidos de muestreos de datos con comportamiento que se supone aleatorio.
El modelo probabilístico como modelo de recuperación de independencia binaria fue desarrollado por Robertson y Spark Jones. Este modelo afirma que pueden caracterizarse los documentos de una colección mediante el uso de términos de indización. Obviamente existe un subconjunto ideal de documentos que contiene únicamente los documentos relevantes a una necesidad de información para la cual se realiza una ponderación de los términos que componen la consulta realizada por el usuario. A continuación el sistema calcula la semejanza entre cada documento de la colección y la consulta y presentando los resultados ordenados por grado de probabilidad de relevancia en la relación a la consulta. Este modelo evita la comparación exacta ( existencia o no de un término de la consulta en el documento) y posibilita al usuario realizar un proceso de retroalimentación valorando la relevancia de los documentos recuperados para que el sistema pueda calcular la probabilidad en posteriores consultas de que los documentos recuperados sean o no relevantes en función de los términos utilizados en la consulta sean o no relevantes.
Pueden ser modelos probabilísticos discretos o continuos. Los primeros, en su mayoría se basan en repeticiones de pruebas de Bernoulli. Los más utilizados son:
Distribución de Bernoulli
En teoría de probabilidad y estadística, la distribución de Bernoulli (o distribución dicotómica), nombrada así por el matemático y científico suizo Jakob Bernoulli, es una distribución de probabilidad discreta, que toma valor 1 para la probabilidad de éxito ( ) y valor 0 para la probabilidad de fracaso (
) y valor 0 para la probabilidad de fracaso ( ).
).
Si  es una variable aleatoria que mide el "número de éxitos", y se realiza un único experimento con dos posibles resultados (éxito o fracaso), se dice que la variable aleatoria
es una variable aleatoria que mide el "número de éxitos", y se realiza un único experimento con dos posibles resultados (éxito o fracaso), se dice que la variable aleatoria  se distribuye como una Bernoulli de parámetro
se distribuye como una Bernoulli de parámetro  .
.
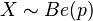
Su función de probabilidad viene definida por:

La fórmula será:
Un experimento al cual se aplica la distribución de Bernoulli se conoce como Ensayo de Bernoulli o simplemente ensayo, y la serie de esos experimentos como ensayos repetidos.
Propiedades características
Esperanza matemática:
Varianza:
Función generatriz de momentos:
Función característica:
Moda:
- 0 si q > p (hay más fracasos que éxitos)
- 1 si q < p (hay más éxitos que fracasos)
- 0 y 1 si q = p (los dos valores, pues hay igual número de fracasos que de éxitos)
Asimetría (Sesgo):
Curtosis:
La Curtosis tiende a infinito para valores de  cercanos a 0 ó a 1, pero para
cercanos a 0 ó a 1, pero para 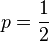 la distribución de Bernoulli tiene un valor de curtosis menor que el de cualquier otra distribución, igual a -2.
la distribución de Bernoulli tiene un valor de curtosis menor que el de cualquier otra distribución, igual a -2.
Distribución de Binomial
En estadística, la distribución binomial es una distribución de probabilidad discreta que cuenta el número de éxitos en una secuencia de n ensayos de Bernoulli independientes entre sí, con una probabilidad fija p de ocurrencia del éxito entre los ensayos. Un experimento de Bernoulli se caracteriza por ser dicotómico, esto es, sólo son posibles dos resultados. A uno de estos se denomina éxito y tiene una probabilidad de ocurrencia p y al otro, fracaso, con una probabilidad q = 1 - p. En la distribución binomial el anterior experimento se repite n veces, de forma independiente, y se trata de calcular la probabilidad de un determinado número de éxitos. Para n = 1, la binomial se convierte, de hecho, en una distribución de Bernoulli.
Para representar que una variable aleatoria X sigue una distribución binomial de parámetros n y p, se escribe:
La distribución binomial es la base del test binomial de significación estadística.
| Distribución binomial | ||
|---|---|---|
 Función de probabilidad |
||
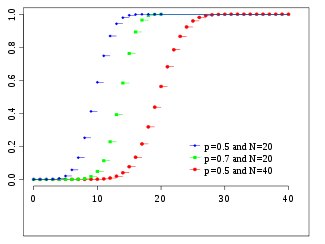 |
| Función de distribución de probabilidad | ||
| Parámetros | 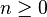 número de ensayos (entero) número de ensayos (entero)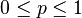 probabilidad de éxito (real) probabilidad de éxito (real) |
|
|---|---|---|
| Dominio | 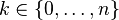 |
|
| Función de probabilidad(fp) | 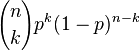 |
|
| Función de distribución(cdf) | 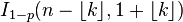 |
|
| Media | 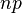 |
|
| Mediana | Uno de 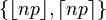 1 1 |
|
| Moda | 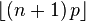 |
|
| Varianza |  |
|
| Coeficiente de simetría | 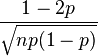 |
|
| Curtosis |  |
|
| Entropía | 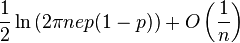 |
|
| Función generadora de momentos(mgf) |  |
|
| Función característica | 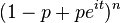 |
|
Distribución de Geométrica
En teoría de probabilidad y estadística, la distribución geométrica es cualquiera de las dos distribuciones de probabilidad discretas siguientes:
· la distribución de probabilidad del número X del ensayo de Bernoulli necesaria para obtener un éxito, contenido en el conjunto { 1, 2, 3,...} o
· la distribución de probabilidad del número Y = X − 1 de fallos antes del primer éxito, contenido en el conjunto { 0, 1, 2, 3,... }.
Cual de éstas es la que uno llama "la" distribución geométrica, es una cuestión de convención y conveniencia.
Propiedades Si la probabilidad de éxito en cada ensayo es p, entonces la probabilidad de que x ensayos sean necesarios para obtener un éxito es
para x = 1, 2, 3,.... Equivalentemente, la probabilidad de que haya x fallos antes del primer éxito es
para x = 0, 1, 2, 3,....
En ambos casos, la secuencia de probabilidades es una progresión geométrica.
El valor esperado de una variable aleatoria X distribuida geométricamente es
y dado que Y = X-1,
En ambos casos, la varianza es
Las funciones generatrices de probabilida de X y la de Y son, respectivamente,funciones generatrices de probabilida
Como su análoga continua, la distribución exponencial, la distribución geométrica carece de memoria. Esto significa que si intentamos repetir el experimento hasta el primer éxito, entonces, dado que el primer éxito todavía no ha ocurrido, la distribución de probabilidad condicional del número de ensayos adicionales no depende de cuantos fallos se hayan observado. El dado o la moneda que uno lanza no tiene "memoria" de estos fallos. La distribución geométrica es de hecho la única distribución discreta sin memoria.
De todas estas distribuciones de probabilidad contenidas en {1, 2, 3,... } con un valor esperado dado μ, la distribución geométrica X con parámetro p = 1/μ es la de mayor entropía.
La distribución geométrica del número y de fallos antes del primer éxito es infinitamente divisible, esto es, para cualquier entero positivo n, existen variables aleatorias independientes Y 1,..., Yn distribuidas idénticamente la suma de las cuales tiene la misma distribución que tiene Y. Estas no serán geométricamente distribuidas a menos que n = 1.
Distribución binomial negativa o de pascal
En estadística la distribución binomial negativa es una distribución de probabilidad discreta que incluye a la distribución de Pascal.
El número de experimentos de Bernoulli de parámetro  independientes realizados hasta la consecución del k-ésimo éxito es una variable aleatoria que tiene una distribución binomial negativa con parámetros ky
independientes realizados hasta la consecución del k-ésimo éxito es una variable aleatoria que tiene una distribución binomial negativa con parámetros ky  .
.
La distribución geométrica es el caso concreto de la binomial negativa cuando k = 1.
Propiedades
Su función de probabilidad es

para enteros x mayores o iguales que k, donde
 .
.
Su media es

si se piensa en el número de fracasos únicamente y

si se cuentan también los k-1 éxitos.
Su varianza es

en ambos casos.
| Distribución binomial negativa | ||
|---|---|---|
| Parámetros |  (real) (real) (real) (real) |
|
| Dominio |  |
|
| Función de probabilidad(fp) |  |
|
| Función de distribución(cdf) |  es la función beta incompleta regularizada es la función beta incompleta regularizada |
|
| Media |  |
|
| Moda |   |
|
| Varianza |  |
|
| Coeficiente de simetría |  |
|
| Curtosis |  |
|
| Función generadora de momentos(mgf) |  |
|
| Función característica |  |
|
Distribución Hipergeométrica
En teoría de la probabilidad la distribución hipergeométrica es una distribución discreta relacionada con muestreos aleatorios y sin reemplazo. Supóngase que se tiene una población de N elementos de los cuales, d pertenecen a la categoría A y N-d a la B. La distribución hipergeométrica mide la probabilidad de obtener x (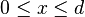 ) elementos de la categoría A en una muestra sin reemplazo de nelementos de la población original.
) elementos de la categoría A en una muestra sin reemplazo de nelementos de la población original.
La función de probabilidad de una variable aleatoria con distribución hipergeométrica puede deducirse a través de razonamientos combinatorios y es igual a
donde  es el tamaño de población,
es el tamaño de población,  es el tamaño de la muestra extraída,
es el tamaño de la muestra extraída,  es el número de elementos en la población original que pertenecen a la categoría deseada y
es el número de elementos en la población original que pertenecen a la categoría deseada y  es el número de elementos en la muestra que pertenecen a dicha categoría. La notación
es el número de elementos en la muestra que pertenecen a dicha categoría. La notación  hace referencia al coeficiente binomial, es decir, el número de combinaciones posibles al seleccionar
hace referencia al coeficiente binomial, es decir, el número de combinaciones posibles al seleccionar  elementos de un total
elementos de un total  .
.
El valor esperado de una variable aleatoria X que sigue la distribución hipergeométrica es
y su varianza,
En la fórmula anterior, definiendo
y
se obtiene
La distribución hipergeométrica es aplicable a muestreos sin reemplazo y la binomial a muestreos con reemplazo. En situaciones en las que el número esperado de repeticiones en el muestreo es presumiblemente bajo, puede aproximarse la primera por la segunda. Esto es así cuando N es grande y el tamaño relativo de la muestra extraída, n/N, es pequeño.
| Distribución hipergeométrica | ||
|---|---|---|
| Parámetros |    |
|
| Dominio |  |
|
| Función de probabilidad(fp) |  |
|
| Media |  |
|
| Moda |  |
|
| Varianza |  |
|
| Coeficiente de simetría | ![\frac{(N-2m)(N-1)^\frac{1}{2}(N-2n)}{[nm(N-m)(N-n)]^\frac{1}{2}(N-2)}](https://upload.wikimedia.org/math/c/b/c/cbc5d8105638f44a15bb6b6a42c98834.png) |
|
| Curtosis |
![+\left.\frac{3n(N-n)(N+6)}{N^2}-6\right]](https://upload.wikimedia.org/math/5/e/e/5eea883c0354dcf5301ca80d816a58c2.png) |
|
| Función generadora de momentos(mgf) |  |
|
| Función característica |  |
|
Distribución Poisson
En teoría de probabilidad y estadística, la distribución de Poisson es una distribución de probabilidad discreta que expresa, a partir de una frecuencia de ocurrencia media, la probabilidad de que ocurra un determinado número de eventos durante cierto período de tiempo. Concretamente, se especializa en la probabilidad de ocurrencia de sucesos con probabilidades muy pequeñas, o sucesos "raros".
La función de masa o probabilidad de la distribución de Poisson es
donde
- k es el número de ocurrencias del evento o fenómeno (la función nos da la probabilidad de que el evento suceda precisamente k veces).
- λ es un parámetro positivo que representa el número de veces que se espera que ocurra el fenómeno durante un intervalo dado. Por ejemplo, si el suceso estudiado tiene lugar en promedio 4 veces por minuto y estamos interesados en la probabilidad de que ocurra k veces dentro de un intervalo de 10 minutos, usaremos un modelo de distribución de Poisson con λ = 10×4 = 40.
- e es la base de los logaritmos naturales (e = 2,71828...)
Tanto el valor esperado como la varianza de una variable aleatoria con distribución de Poisson son iguales a λ. Los momentos de orden superior son polinomios de Touchard en λ cuyos coeficientes tienen una interpretación combinatorio. De hecho, cuando el valor esperado de la distribución de Poisson es 1, entonces según la fórmula de Dobinski, el n-ésimo momento iguala al número de particiones de tamaño n.
La moda de una variable aleatoria de distribución de Poisson con un λ no entero es igual a 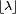 , el mayor de los enteros menores que λ (los símbolos
, el mayor de los enteros menores que λ (los símbolos  representan la función parte entera). Cuando λ es un entero positivo, las modas son λ y λ − 1.
representan la función parte entera). Cuando λ es un entero positivo, las modas son λ y λ − 1.
La función generadora de momentos de la distribución de Poisson con valor esperado λ es
Las variables aleatorias de Poisson tienen la propiedad de ser infinitamente divisibles.
La divergencia Kullback-Leibler desde una variable aleatoria de Poisson de parámetro λ0 a otra de parámetro λ es
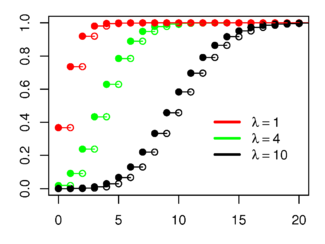
Distribución de Poisson Plot of the Poisson PMF
El eje horizontal es el índice x. La función solamente está definida en valores enteros de k. Las líneas que conectan los puntos son solo guías para el ojo y no indican continuidad.
Función de probabilidad
El eje horizontal es el índice k.
Función de distribución de probabilidadParámetros Dominio Función de probabilidad(fp) Función de distribución(cdf) (dónde
es laFunción gamma incompleta)
Media Mediana Moda Varianza Coeficiente de simetría Curtosis Entropía Función generadora de momentos(mgf) Función característica [editar datos en Wikidata]
Por otro lado, tal como se ha mencionado antes, existen modelos probabilísticos continuos, entre ellos destacamos:
En estadística y probabilidad se llama distribución normal, distribución de Gauss o distribución gaussiana, a una de las distribuciones de probabilidad de varible continua que con más frecuencia aparece aproximada en fenómenos reales.
La gráfica de sufuncion densidad tiene una forma acampanada y es simétrica respecto de un determinado parámetro estadístico. Esta curva se conoce como campana de Gauss y es el gráfico de una función gaussiana.
La importancia de esta distribución radica en que permite modelar numerosos fenómenos naturales, sociales y psicológicos. Mientras que los mecanismos que subyacen a gran parte de este tipo de fenómenos son desconocidos, por la enorme cantidad de variables incontrolables que en ellos intervienen, el uso del modelo normal puede justificarse asumiendo que cada observación se obtiene como la suma de unas pocas causas independientes.
De hecho, la estadística descriptiva sólo permite describir un fenómeno, sin explicación alguna. Para la explicación causal es preciso el diseño experimental, de ahí que al uso de la estadística en psicología y sociología sea conocido como método correlacional.
La distribución normal también es importante por su relación con la estimación por mínimos cuadrados , uno de los métodos de estimación más simples y antiguos.
Algunos ejemplos de variables asociadas a fenómenos naturales que siguen el modelo de la normal son:
· caracteres morfológicos de individuos como la estatura ;
· caracteres fisiológicos como el efecto de un fármaco;
· caracteres sociológicos como elconsumo de cierto producto por un mismo grupo de individuos;
· caracteres psicológicos como el cociente intelectual;
· nivel de ruido en telecomunicaciones;
· errores cometidos al medir ciertas magnitudes;
· etc.
La distribución normal también aparece en muchas áreas de la propia estadística. Por ejemplo, la distrución muestral de las medias muestrales es aproximadamente normal, cuando la distribución de la población de la cual se extrae la muestra no es normal.1 Además, la distribución normal maximiza la entropía entre todas las distribuciones con media y varianza conocidas, lo cual la convierte en la elección natural de la distribución subyacente a una lista de datos resumidos en términos de media muestral y varianza. La distribución normal es la más extendida en estadística y muchos tests estadísticos están basados en una supuesta "normalidad".
En probabilidad, la distribución normal aparece como el límite de varias distribuciones de probabilidad continuas y discretas.| Distribución normal | ||
|---|---|---|
 La línea verde corresponde a la distribución normal estándar Función de densidad de probabilidad |
||
 Función de distribución de probabilidad |
||
| Parámetros |
 |
|
| Dominio |  |
|
| Función de densidad(pdf) |  |
|
| Función de distribución (cdf) |  |
|
| Media |  |
|
| Mediana |  |
|
| Moda |  |
|
| Varianza |  |
|
| Coeficiente de simetría | 0 | |
| Curtosis | 0 | |
| Entropía |  |
|
| Función generadora de momentos (mgf) |  |
|
| Función característica |  |
|
—————

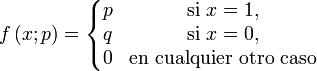
![E\left[X\right] = p = u](https://upload.wikimedia.org/math/7/0/b/70b7ee43476e53039eac126116ee0161.png)
![var\left[X\right] = p \left(1 - p\right) = p q](https://upload.wikimedia.org/math/b/c/8/bc80ba4ce849763cc532daedbc7d2f46.png)


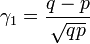
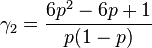

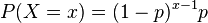






![E[X]=\frac{nd}{N}](https://upload.wikimedia.org/math/e/d/b/edb7931c237719680795389c71e2ca37.png)
![Var[X]=\bigg(\frac{N-n}{N-1}\bigg)\bigg(\frac{nd}{N}\bigg)\bigg( 1-\frac{d}{N}\bigg).](https://upload.wikimedia.org/math/9/b/2/9b21150dd51ee2e8e3c219b9d6c67cdd.png)


![Var[X]=npq\frac{N-n}{N-1}.](https://upload.wikimedia.org/math/8/4/5/8450776365971ac3ed36f95d91b68b22.png)
![\left[\frac{N^2(N-1)}{n(N-2)(N-3)(N-n)}\right]](https://upload.wikimedia.org/math/b/5/c/b5c85bfac379f6390cf9ac846b3643cc.png)







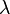




![\lambda[1\!-\!\ln(\lambda)]\!+\!e^{-\lambda}\sum_{k=0}^\infty \frac{\lambda^k\ln(k!)}{k!}](https://upload.wikimedia.org/math/3/6/f/36f5766e9855c58b14b1b542b27c7812.png)


