Variables aleatorias conjuntas (teoría)
Puedes descargar el tema completo aquí:Tema_5.pdf (790236)
función Densidad Conjunta ó f.d.p Conjunta
El estudio de variables aleatorias y su distribución de probabilidad, en lo aprendido anteriormente ha estado restringido a espacios muéstrales unidimensionales en los que registramos los resultados asumidos por una sola variable en un experimento. Sin embargo habrá situaciones en las que convenga registrar resultados simultáneos de diferentes variables aleatorias.
Definición:
Se dice que dos variables aleatorias X e Y tienen una distribución continua conjunta si existe una función NO negativa f definida sobre todo el plano xy tal que para cualquier subconjunto A del plano,
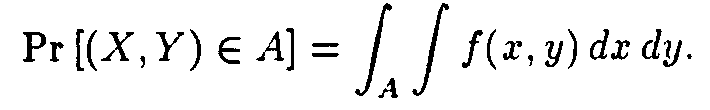
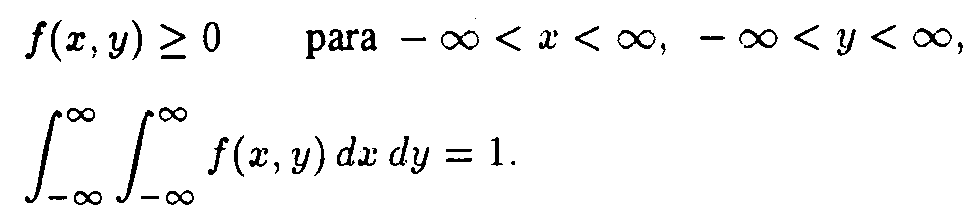
La probabilidad de que el par (X,Y) pertenezca a cualquier región del plano xy se puede determinar integrando la f.d.p conjunta f(x,y) sobre esa región.
EL volumen total por debajo de la superficie z =f(x, y) y por encima del plano xy debe ser 1. La probabilidad de que el par (X, Y) pertenezca al rectángulo A es igual al volumen de la figura sólida con base que se muestra a continuación. La parte superior de la figura sólida está formada por la superficie z = f(x, y).
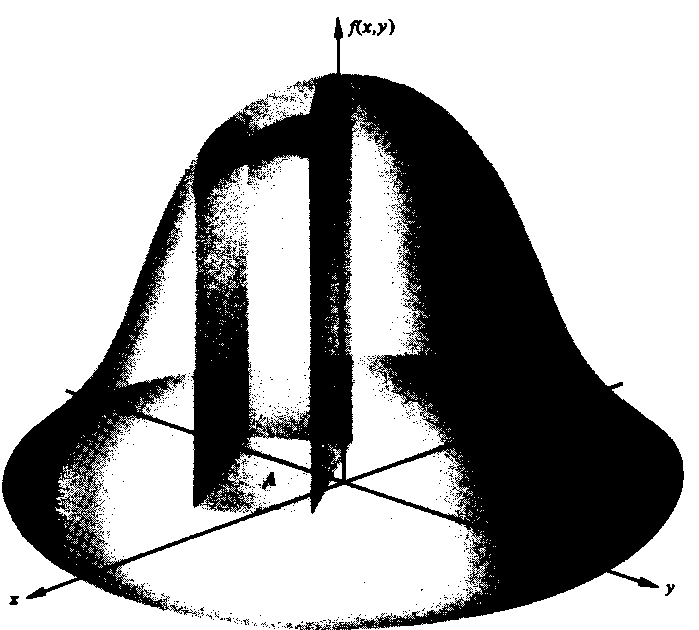
Ejemplo:
-
En un estudio para determinar la posibilidad de graduación en una universidad, basado en datos de estudios anteriores, debemos usar un espacio bidimensional y registrar para cada individuo el resultado de su examen de aptitud y las calificaciones de bachillerato.
-
Podemos medir la cantidad de precipitado P y el volumen V de un gas, generado durante un experimento químico controlado, teniendo así un espacio muestral (p, v).
-
También se puede medir la dureza D y el esfuerzo a la tensión T del cobre estruido en frío cuyo resultado son (d, t).
Función Densidad Marginal
En la parte anterior observamos que si se conoce la f.d. conjunta F de dos variables aleatorias X e Y, entonces se puede obtener la f.p. F1 de la variable aleatoria X a partir de F. En este contexto en que la distribución de X se obtiene a partir de la distribución conjuntas de X e Y, F1 se denomina f.d marginal de X. Análogamente, si se conoce la f.p. conjunta o la f.d.p conjunta de X e Y, entonces se puede obtener la f.p marginal o f.d.p. marginal de cada variable aleatoria a partir de .
Aquí hay que tener cuidado, ya que cuando se calcula la densidad conjunta, hay que fijarse bien en el dominio de las otras variables.
Las funciones de densidad de probabilidad marginal de X y Y, denotadas por X (X) y Y(Y) , respectivamente, están dada por
X(X) = f(x, y)dy, para -"
a) Hallar la funci´on de densidad conjunta de (X, Y ) .
b) Calcular P (Y _ X) .
c) Hallar las funciones de densidad marginales fX y fY .
Función Densidad Condicional ó f.d.p Condicional.
Definición:
Sean X y Y dos v.a continuas con p.d.f f(x, y) conjunta y p.d.f f x(x) marginal X. Entonces, para cualquier valor x de X para el que fx(x) >0, la función de densidad de probabilidad condicional de Y, dado que X = x es:
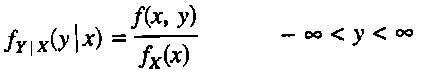
Características:
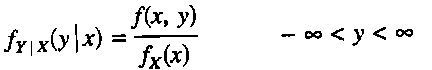
-
a definición

es paralela a la P(B | A), que es la probabilidad condicional de que B ocurra, dado que A ha ocurrido. -
La f.d.p Condicional g1(x|y) de X debe ser proporcional a f(x, yo). En otras palabras, g1(x|y) es esencialmente igual que f(x, yo), pero incluye un factor constante 1/ [f2(yo)] que se necesita para que la integral de la f.d.p condicional sobre todos los valores de X sea la unidad.
Uso:
Sirve para estudiar la posibilidad de que ocurra un X, bajo la ocurrencia de Y; o viceversa.
Ejercicios:
Suponga que X= el número de defectos críticos en un automóvil nuevo seleccionado al azar y Y= al número de defectos de poca importancia en ese mismo automóvil. Si sabemos que el numero de defectos críticos en el automóvil seleccionado es 1, ¿Cuál es la probabilidad de que el automóvil tenga a lo sumo tres defectos de poca importancia?, es decir,
¿Cuál es P(Y<= 3 | X = 1 )? Análogamente, si X e Y denotan las duraciones de dos componentes de un sistema y resulta que X = 100, ¿Cuál es la probabilidad de que Y>=200?, y cual es la duración esperada del segundo componente “condicionado” a este valor X?
—————
